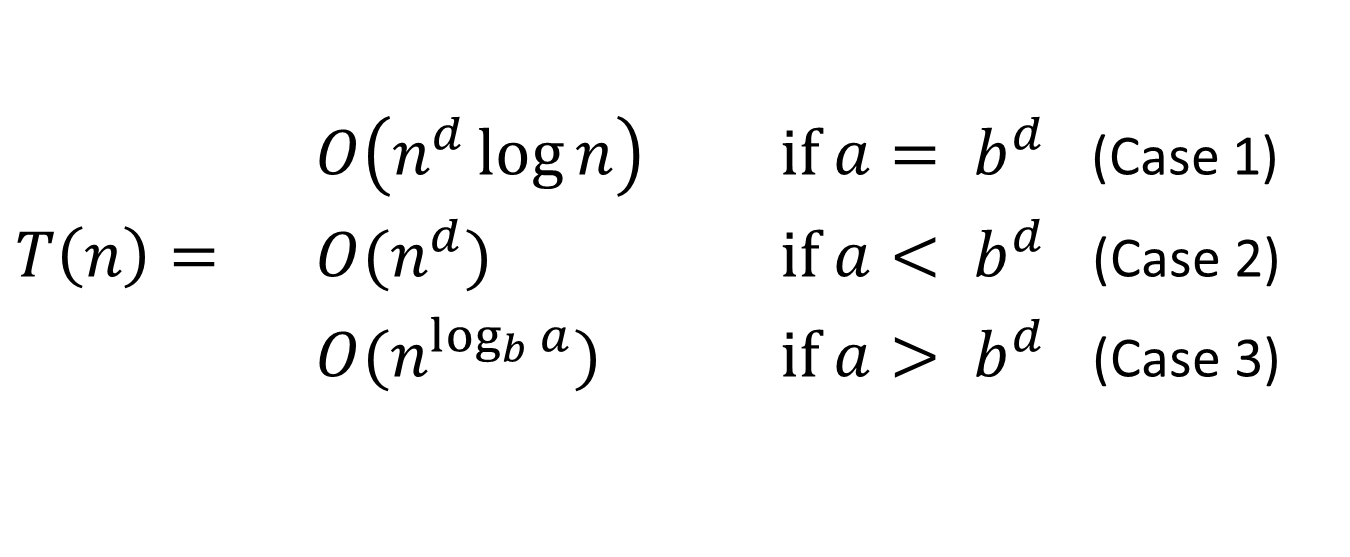notes

Algorithms

Guiding Principles for Analysis of Algorithms

1. Use worst-case analysis
2. Do not pay much attention to constant factors, lower-order terms
   • it is way easier
   • constants depend on architecture/compiler/programmer anyway
   • lose very little predictive power
3. Use asymptocit analysis (focus on large input sizes)
4. Fast Algorithm - worst-case running time grows slowly with input size
5. Big O - T(n) = O(f(n)) if and only if there exist constants c, k > 0 such that T(n)<=cf(n) for all n >= k

The Divide and Conquer Paradigm

1. Divide into smaller subproblems
2. Conquer via recursive calls
3. Combine solutions of subpromlems into one for the original problem

Counting inversions

1. Inversion - when there is an array a and a[i] > a[j] && i < j

2. There are the following types of inversion:
   • left inversion if i, j <= n\2
   • right inversin if i, j > n\2
   • split inversion if i <= n\2 < j
3. Pseudo code

  if n = 1 return 0
  else
    x = Count (1st half of a, n\2)
    y = Count (2nd half of a, n\2)
    z = CountSplitInversions (a, n)

    return x + y + z

1. Key idea to count split inversion: have recursive calls both count inversions and sort. Motivation: Merge subroutine naturally uncovers split inversions.

The Master method

1. Master method - “black box” for solving recurrences.
2. Assumption: all subproblems have equal size
3. T(n) - maximum running time of the algorithm
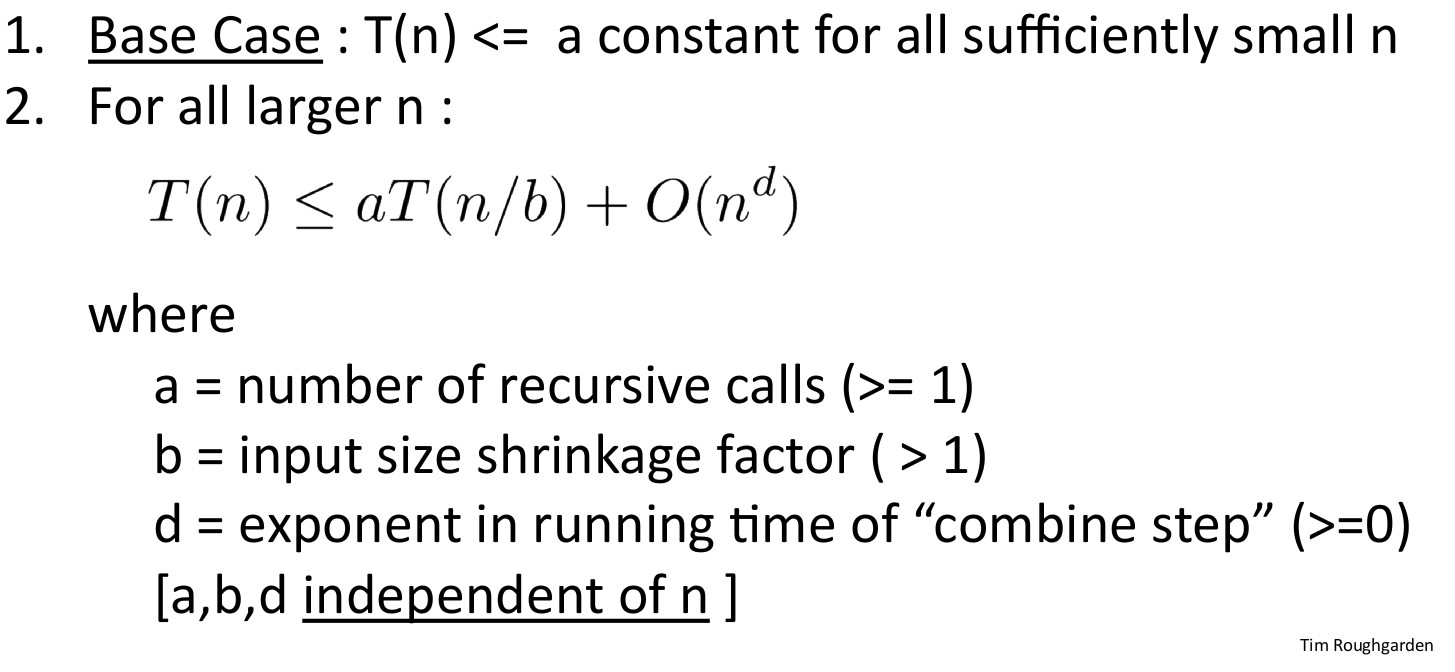4. IF: THEN: